Множеството е първично понятие в математиката.
Обектите, от които се състои дадено множество се наричат още негови елементи. Множествата означаваме с различни главни букви от латинската азбука – M, N, P, Q, R,…, а елементите им – с малки букви от една и същата азбука – a, b, c, d,…
Множество, което се състои от краен брой елементи, се нарича крайно.
Множество, което се състои от безброй много елементи, се нарича безкрайно.
Множество, което не съдържа елементи, изучавани в дадена теория, се нарича универсално множество, съответно на тази теория, и се означава с U.
Множество, което се състои от точки се нарича точково множество.
Множество, чиито елементи са числа, се нарича числово множество. Например множеството на целите числа, множеството на дробните числа, множеството на числата, които се делят на 2 и прочие, са числови множества, а всяка фигура може да се разглежда като точково множество.
Твърдението „а е елемент (принадлежи) на множеството М“ се записва символично така: a принадлежи M.
Твърдението „a не е елемент (не принадлежи) на множеството N” се записва символично така:
A не принадлежи N.
Операции с множества
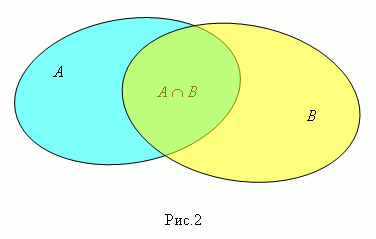
Ако A и B са две множества, то множеството C, което се състои от елементите, принадлежащи и на A, и на B, се нарича сечение на A и B и се записва символично така:
C = A n B
Ако M и N са две множества, то множеството P, което се състои от елементите, принадлежащи поне на едно от множествата M и N< се нарича обединение на M и N и се записва символично така:
P = M u N.
Ако R и P са две множества, то множеството L, което се състои от тези елементи на R, които не принадлежат на P, се нарича разлика на R и P и се записва символично така:
L=R\P.